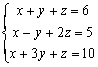
Ńp•Ŗ§G/§T§ł§@¶ł§ŤĶ{(•]¨A≥qł—)§ő¶ś¶C¶°(II)
Ķ{¶°®Ō•ő§FßJĶ‹ļŅ™kęh (Cramer's rule)°A¶]¶ĻłŻ§@ĮŽ®Ō•őģÝ•h™k™ļĶ{¶°°A∑«ĹTę◊ī£į™§F°A¶”•BĶ{¶°™ļ≠≠®ÓĪÝ•ů•ÁłŻ§÷°CĶ{¶°į£§F•i•H≠pļ‚Ńp•Ŗ§T§ł§@¶ł§ŤĶ{™ļģŕ§ő¶ś¶C¶°•~°AŃŔ•i•H≠pļ‚Ńp•Ŗ§T§ł§@¶ł§ŤĶ{™ļ≥qł—§őŃp•Ŗ§G§ł§@¶ł§ŤĶ{™ļģŕ °CĶ{¶°ŃŲĶMłŻ≤ń(I)™©™Ý§@¬I°A¶ż≥qł—®Ō•ő§F§@ĮÍ≤ŖļD™ļ§Ť™k(z=t)°A•t•~Ķ{¶°ßů•i•Hįt¶X§pľ∆¬ŗīę§ņľ∆Ķ{¶°(III)™ļ≤ń§G≠”Ķ{¶°ĪN§ŤĶ{™ļł—(•]¨A≥qł—)¬ŗ§∆¨į§ņľ∆°C
Ķ{¶°Ĺsľg§ťīŃ: 2007¶~2§Ž3§ť
Ķ{¶°(116®B)
| 1 | ENT | 2. | Kin 2 | 3. | ENT | 4. | Kin 1 | 5. | Kin 5 |
| 6. | ENT | 7. | Kin 3 | 8. | ENT | 9. | Kin 4 | 10. | ENT |
| 11. | + | 12. | ( | 13. | ENT | 14. | Kin 6 | 15. | °— |
| 16. | Kout 3 | 17. | - | 18. | ENT | 19. | Kin °— 5 | 20. | X°Ų°ųK5 |
| 21. | ) | 22. | +/- | 23. | Min | 24. | 0 | 25. | = |
| 26. | Kin °— 3 | 27. | X°Ų°ųK2 | 28. | Kin °— 5 | 29. | X°Ų°ųK5 | 30. | Kin - 3 |
| 31. | Kout 5 | 32. | X°Ų°ųK6 | 33. | Kin °— 6 | 34. | X°Ų°ųK4 | 35. | Kin °— 4 |
| 36. | X°Ų°ųK2 | 37. | Kin °— 2 | 38. | X°Ų°ųK1 | 39. | Kin °— 1 | 40. | °— |
| 41. | Kout 1 | 42. | Kin - 6 | 43. | ENT | 44. | Kin °— 5 | 45. | = |
| 46. | Kin - 4 | 47. | Kout 2 | 48. | Kin - 5 | 49. | Kout 4 | 50. | °“ |
| 51. | Kout 6 | 52. | = | 53. | ENT | 54. | Kin 1 | 55. | °— |
| 56. | MR | 57. | + | 58. | Kout 5 | 59. | X°Ų°ųK6 | 60 | Kin °“ 6 |
| 61. | X°Ų°ųK6 | 62. | Kin 2 | 63. | ENT | 64. | Kin 2 | 65. | °— |
| 66. | Kout 3 | 67. | + | 68. | MR | 69. | X°Ų°ųK6 | 70. | Kin °“ 6 |
| 71. | X°Ų°ųK6 | 72. | Min | 73. | ENT | 74. | °— | 75. | Kout 6 |
| 76. | = | 77 | X°Ų°ųK4 | 78. | Kin °— 1 | 79. | X°Ų°ųK2 | 80. | X°Ų°ųK5 |
| 81. | Kin °— 5 | 82. | X°Ų°ųK5 | 83. | Kin + 1 | 84. | Kout 3 | 85. | °“ |
| 86. | Kout 6 | 87. | = | 88. | ENT | 89. | X°Ų°ųK6 | 90. | Kin °— 6 |
| 91. | X°Ų°ųK6 | 92. | Kin - 1 | 93. | Kout 4 | 94. | HLT | 95. | +/- |
| 96. | Kin °“ 1 | 97. | Kout 1 | 98. | Kin °— 3 | 99. | °— | 100. | MR |
| 101. | °— | 102. | Kout 6 | 103. | = | 104. | Kin + 2 | 105. | Kout 5 |
| 106. | Kin + 3 | 107. | Kout 6 | 108. | Kin °“ 3 | 109. | Kin °“ 2 | 110. | Kout 2 |
| 111. | HLT | 112. | X°Ų°ųK1 | 113. | X°Ų°ųK3 | 114. | Kin 2 | 115. | HLT |
| 116. | Kout 3 | 117. | °@ | 118. | °@ | 119. | °@ | 120. | °@ |
LRN ľ“¶°Ņť§JĶ{¶°(®— fx-3600PV§őfx-3800P®Ō•ő°AĶ{¶°™Ýę◊: 116®B )
| ENT 1 | Kin 2 | ENT 1 | Kin 1 | Kin 5 |
| ENT 1 | Kin 3 | ENT 1 | Kin 4 | ENT 0 |
| + | ( | ENT 1 | Kin 6 | °— |
| Kout 3 | - | ENT 1 | Kin °— 5 | X°Ų°ųK5 |
| ) | +/- | Min | 0 | = |
| Kin °— 3 | X°Ų°ųK2 | Kin °— 5 | X°Ų°ųK5 | Kin - 3 |
| Kout 5 | X°Ų°ųK6 | Kin °— 6 | X°Ų°ųK4 | Kin °— 4 |
| X°Ų°ųK2 | Kin °— 2 | X°Ų°ųK1 | Kin °— 1 | °— |
| Kout 1 | Kin - 6 | ENT 1 | Kin °— 5 | = |
| Kin - 4 | Kout 2 | Kin - 5 | Kout 4 | °“ |
| Kout 6 | = | ENT 1 | Kin 1 | °— |
| MR | + | Kout 5 | X°Ų°ųK6 | Kin °“ 6 |
| X°Ų°ųK6 | Kin 2 | ENT 2 | Kin 2 | °— |
| Kout 3 | + | MR | X°Ų°ųK6 | Kin °“ 6 |
| X°Ų°ųK6 | Min | ENT 3 | °— | Kout 6 |
| = | X°Ų°ųK4 | Kin °— 1 | X°Ų°ųK2 | X°Ų°ųK5 |
| Kin °— 5 | X°Ų°ųK5 | Kin + 1 | Kout 3 | °“ |
| Kout 6 | = | ENT 4 | X°Ų°ųK6 | Kin °— 6 |
| X°Ų°ųK6 | Kin - 1 | Kout 4 | HLT | +/- |
| Kin °“ 1 | Kout 1 | Kin °— 3 | °— | MR |
| °— | Kout 6 | = | Kin + 2 | Kout 5 |
| Kin + 3 | Kout 6 | Kin °“ 3 | Kin °“ 2 | Kout 2 |
| HLT | X°Ų°ųK1 | X°Ų°ųK3 | Kin 2 | HLT |
| Kout 3 | MODE . | °@ | °@ | °@ |
Ķý: ≠Y§ŤĶ{≤’¨į a1x + b1y + c1z = d1 , a2x + b2y + c2z = d2 , a3x + b3y + c3z = d3
Ķ{¶°™ļ≠≠®ÓĪÝ•ů¨į: a1b2°ŕa2b1°A≠Y™G§ŤĶ{≤’™ļ¶ś¶C¶°Ň„•‹¨įĻs°A™Ū•‹§ŤĶ{ĶLįŖ§@ł—(ĶL≠≠ł—©őĶLł—)°A Ķ{¶°∑|¶bŇ„•‹¶ś¶C¶°ľ∆≠»ęŠ•X≤{-E-°C≠Y™G•u¨OŅť§J™ļľ∆ĺŕĻH§Ō≠≠®ÓĪÝ•ů°Aęh∑|¶b Ņť§J≤ń§G≤’§ŤĶ{ꊰAĶ{¶°§~∑|•X≤{-E-°A≥oģ…Ĺ–ĪN§ŤĶ{≤’§ļ™ļ§ŤĶ{¶°Ĺ’ī궳߫Ņť§J°C
°@
®“√D1: ł—Ńp•Ŗ§ŤĶ{ :
ęŲ P1 ¶AęŲ 1 RUN 1 RUN 1 RUN 6 RUN 1 RUN 1 +/- RUN 2 RUN 5 RUN 1 RUN
3 RUN 1 RUN 10 RUN (•żŇ„•‹§ŤĶ{≤’¶ś¶C¶°™ļ≠»¨į - 2)
RUN (Ň„•‹x=1) RUN (Ň„•‹y=2) RUN (Ň„•‹z=3)
Ķ{¶°įű¶śßĻ¶®ęŠAC≤◊§ÓĶ{¶°°AęŲ Kout 1°BKout 2°BKout 3§őKout 4§ņßOŇ„•‹x°By°Bz™ļ≠»§ő§ŤĶ{≤’¶ś¶C¶°™ļ≠»°C
Ķý1: Ķ{¶°•i•Hįt¶X§pľ∆¬ŗīę§ņľ∆Ķ{¶°(III)™ļ≤ń§G≠”Ķ{¶°°AĪNŃp•Ŗ§T§ł§@¶ł§ŤĶ{™ļł—¬ŗ§∆¨į§ņľ∆°C™`∑N: ¬ŗ§∆ģ…°AĹ–•ż¬ŗ§∆ł—Ķ™z≠»°A¬ŗ§∆ęŠ z≠»™ļįOĺ–(K3)§ő¶ś¶C¶°™ļįOĺ–(K4)ęh§£ĮŗęOĮd°A§ßꊶAęŲ Kout 1(©őKout 2)ī£®ķ x™ļ≠» (©ő y™ļ≠») ¬ŗ§∆¨į§ņľ∆°C
°@
®“√D2: ł—•H§UŃp•Ŗ§G§ł§@¶ł§ŤĶ{
![]()
Ņť§Jģ…•u≠n§£Ņť§Jz™ļęYľ∆ßY•i
ęŲ P1 ¶AęŲ 1 RUN 1 RUN RUN (§£Ņť§Jľ∆≠») 7 RUN
1 RUN -1 RUN RUN (§£Ņť§Jľ∆≠») 1 RUN (Ň„•‹4) RUN (Ň„•‹3)
¶]¶Ļł—Ķ™¨į x = 4 §ő y = 3.
≠p
ļ‚ßĻĶ≤°AĹ–ęŲAC§§§ÓĶ{¶° °Ax™ļ≠»°By™ļ≠»§ő§ŤĶ{≤’¶ś¶C¶°™ļ≠»§ņßOņx¶s©ůįOĺ–K1°BK2§őK6§§°CĶý2: ¶b≤◊§ÓĶ{¶°ęŠ°A•iĪNł—Ķ™¬ŗ§∆¨į§ņľ∆°A•ięŲ Kout 1 (©ő Kout 2)ī£®ķ x≠»(©ő y≠»)∂i¶ś¬ŗ§∆ßY•i°A¶ż¶ś¶C¶°™ļįOĺ–(K6)ęh§£ĮŗęOĮd°C
°@
®“√D3: ≠pļ‚§U¶C™ļ¶ś¶C¶°:°@
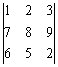
Ņť§Jģ…•u≠n§£Ņť§JĪ`ľ∆∂ĶßY•i
ęŲ P1 ¶AęŲ 1 RUN 2 RUN 3 RUN RUN (§£Ņť§Jľ∆≠»)
7 RUN 8 RUN 9 RUN RUN (§£Ņť§Jľ∆≠»)
6 RUN 5 RUN 2 RUN RUN (§£Ņť§Jľ∆≠»°AŇ„•‹¶ś¶C¶°™ļ≠»¨į12)
Ķ{¶°įű¶śßĻ¶®ęŠ°AĹ–ęŲAC§§§ÓĶ{¶°°C¶ś¶C¶°™ļ≠»ņx¶s©ůįOĺ–K4°C
°@
®“√D4: ®D§U¶CŃp•Ŗ§ŤĶ{™ļ≥qł—:
![]()
ęŲ P1 ¶AęŲ - 7 RUN 1 RUN 1 RUN 3 RUN 1 RUN -1 RUN 1 RUN 1 RUN
(Ň„•‹ x™ļł—°AĪ`ľ∆∂Ķ¨į - 0.666666666)
RUN (Ň„•‹ y™ļł—°AĪ`ľ∆∂Ķ¨į -1.666666667)
RUN (Ň„•‹ x™ļł—°At™ļęYľ∆¨į 0.333333333)
RUN (Ň„•‹ y™ļł—°At™ļęYľ∆¨į 1.333333333)
¶]¶Ļ≥qł—¨į:
x = - 0.666666666 + 0.333333333 t
y = - 1.666666666 + 1.333333333 t
z = t
≠Y™G§£•őĪNł—Ķ™¬ŗ§ņľ∆°AĹ–ęŲ AC ≤◊§ÓĶ{¶°°Aß_ęh™ĹĪĶįű¶ś§pľ∆¬ŗīę§ņľ∆(III)Ķ{¶°•ż¬ŗ§∆≥Őꊙļľ∆≠»(y™ļł— tęYľ∆)°A®šĺl§T≠”≥qł—™ļľ∆≠»§ņßOįO¶s¶bK1°BK2§őM§§°A•u≠nī£®ķľ∆≠»¶A∂i¶ś¬ŗ§∆ßY•i°C
°@