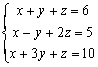
�p�ߤG/�T���@����{(�]�A�q��)�Φ�C��(I)
�{���ϥΤF�J�ܺ��k�h (Cramer's rule)�A�]�����@��ϥή��h�k���{���A�ǽT�״����F�A�ӥB�{��������������֡C�{�����F�i�H�p���p�ߤT���@����{���ڤΦ�C���~�A�٥i�H�p���p�ߤT���@����{���q�Ѥ��p�ߤG���@����{���� �A�{����i�H�t�X�p���ഫ����(II)���p���ഫ���Ƶ{��(III)���ĤG�ӵ{���N��{����(���]�A�q��)��Ƭ����ơC�C
�{���s�g���: 2006�~10��1��
�{��(104�B)
| 1 | ENT | 2. | Kin 2 | 3. | ENT | 4. | Kin 1 | 5. | Kin 5 |
| 6. | ENT | 7. | Kin 3 | 8. | ENT | 9. | Kin 4 | 10. | ENT |
| 11. | Kin �� 5 | 12. | X����K5 | 13. | Min | 14. | ENT | 15. | Kin 6 |
| 16. | �� | 17. | Kout 2 | 18. | M- | 19. | ENT | 20. | Kin �� 2 |
| 21. | X����K3 | 22. | Kin �� 5 | 23. | X����K5 | 24. | Kin - 2 | 25. | Kout 5 |
| 26. | X����K6 | 27. | Kin �� 6 | 28. | X����K4 | 29. | Kin �� 4 | 30. | X����K3 |
| 31. | Kin �� 3 | 32. | X����K1 | 33. | Kin �� 1 | 34. | �� | 35. | Kout 1 |
| 36. | Kin - 6 | 37. | ENT | 38. | Kin �� 5 | 39. | = | 40. | Kin - 4 |
| 41. | Kout 3 | 42. | Kin - 5 | 43. | Kout 5 | 44. | Kin 1 | 45. | Kout 4 |
| 46. | Kin 3 | 47. | Kout 6 | 48. | Kin �� 1 | 49. | Kin �� 3 | 50. | +/- |
| 51. | �� | 52. | Kout 1 | 53. | ENT | 54. | - | 55. | Kout 3 |
| 56. | ENT | 57. | Kin 3 | 58. | �� | 59. | Kout 2 | 60 | - |
| 61. | ( | 62. | Kout 2 | 63. | �� | 64. | Kout 6 | 65. | ) |
| 66. | ENT | 67. | Kin 1 | 68. | �� | 69. | MR | 70. | = |
| 71. | X����K4 | 72. | Kin �� 1 | 73. | X����K3 | 74. | �� | 75. | Kout 5 |
| 76. | - | 77 | ( | 78. | MR | 79. | �� | 80. | Kout 6 |
| 81. | ) | 82. | ENT | 83. | �� | 84. | Kout 6 | 85. | = |
| 86. | Kin + 1 | 87. | Kout 4 | 88. | Kin �� 1 | 89. | HLT | 90. | Kout 1 |
| 91. | Kin �� 2 | 92. | HLT | 93. | �� | 94. | MR | 95. | = |
| 96. | Kin + 3 | 97. | Kout 5 | 98. | Kin + 2 | 99. | Kout 6 | 100. | Kin �� 2 |
| 101. | Kin �� 3 | 102. | Kout 2 | 103. | HLT | 104. | Kout 3 | 105. | �@ |
LRN �Ҧ���J�{��(�� fx-3800P�ϥΡA�{������: 104�B )
| ENT 1 | Kin 2 | ENT 1 | Kin 1 | Kin 5 |
| ENT 1 | Kin 3 | ENT 1 | Kin 4 | ENT 1 |
| Kin �� 5 | X����K5 | Min | ENT 0 | Kin 6 |
| �� | Kout 2 | M- | ENT 1 | Kin �� 2 |
| X����K3 | Kin �� 5 | X����K5 | Kin - 2 | Kout 5 |
| X����K6 | Kin �� 6 | X����K4 | Kin �� 4 | X����K3 |
| Kin �� 3 | X����K1 | Kin �� 1 | �� | Kout 1 |
| Kin - 6 | ENT 1 | Kin �� 5 | = | Kin - 4 |
| Kout 3 | Kin - 5 | Kout 5 | Kin 1 | Kout 4 |
| Kin 3 | Kout 6 | Kin �� 1 | Kin �� 3 | +/- |
| �� | Kout 1 | ENT 1 | - | Kout 3 |
| ENT 2 | Kin 3 | �� | Kout 2 | - |
| ( | Kout 2 | �� | Kout 6 | ) |
| ENT 3 | Kin 1 | �� | MR | = |
| X����K4 | Kin �� 1 | X����K3 | �� | Kout 5 |
| - | ( | MR | �� | Kout 6 |
| ) | ENT 4 | �� | Kout 6 | = |
| Kin + 1 | Kout 4 | Kin �� 1 | HLT | Kout 1 |
| Kin �� 2 | HLT | �� | MR | = |
| Kin + 3 | Kout 5 | Kin + 2 | Kout 6 | Kin �� 2 |
| Kin �� 3 | Kout 2 | HLT | Kout 3 | MODE . |
�@
���D1: ���p�ߤ�{ :
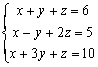
�� P1 �A�� 1 RUN 1 RUN 1 RUN 6 RUN 1 RUN 1 +/- RUN 2 RUN 5 RUN 1 RUN
3 RUN 1 RUN 10 RUN (����覡�զ�C�����Ȭ� - 2)
RUN (���x=1) RUN (���y=2) RUN (���z=3)
�{�����槹�����A�� Kout 1�BKout 2�BKout 3��Kout 4���O���x�By�Bz���ȤΤ�{�զ�C�����ȡC
�@
���D2: �ѥH�U�p�ߤG���@����{
![]()
�� P1 �A�� RUN (����J�ƭ�) 1 RUN 1 RUN 7 RUN
RUN (����J�ƭ�) 1 RUN -1 RUN 1 RUN (���4) RUN (���3)
�]���ѵ��� x = 4 �� y = 3.
�p
�⧹���A����AC����{��x���ȡBy���ȤΤ�{�զ�C�����Ȥ��O�x�s��O��K1�BK3��K6���C
�@
���D3: �p��U�C����C��:�@
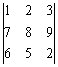
�� P1 �A�� 1 RUN 2 RUN 3 RUN RUN (����J�ƭ�)
7 RUN 8 RUN 9 RUN RUN (����J�ƭ�)
6 RUN 5 RUN 2 RUN RUN (����J�ƭȡA��ܦ�C�����Ȭ�12)
�{�����槹�����A����AC����{���C��C�������x�s��O��K4�C
�@
���D4: �D�U�C�p�ߤ�{���q��:
![]()
�� P1 �A�� - 7 RUN 1 RUN 1 RUN 3 RUN 1 RUN -1 RUN 1 RUN 1 RUN
(���y���ѡA�`�ƶ��� 1)
RUN (���z���ѡA�`�ƶ��� 2)
RUN (���y���ѡAt���Y�Ƭ� 4)
RUN (���z���ѡAt���Y�Ƭ� 3)
�]���q�Ѭ�:
x = t
y = 1 + 4t
z = 2 + 3t
�Ы� AC �פ�{��
�@
��1: �Y��{�լ� a1x + b1y + c1z = d1 , a2x + b2y + c2z = d2 , a3x + b3y + c3z = d3
�{�����������: b1c2��b2c1�A�Y�G��{�ժ���C����ܬ��s�A���ܤ�{�L�ߤ@��(�L���ѩεL��)�A �{���|�b��ܦ�C����X�{-E-�C�Y�G�u�O��J���ƾڹH����������A�h�|�b ��J�ĤG�դ�{��X�{-E-�A�бN��{�դ�����{���մ����ǿ�J �Y�i�C
��2: �{���|�b��J�̫�ƾګe��ܤ�{�զ�C�����ȡA�Y�G���ݭn�{�����椤��ܳo�ӼƭȡA�������{�� �X�i�H����J(�{�������ܬ�103�B)�A��C�����ƭȫh�ݭn�ۦ��Kout 4��ܡC
��3: �{���i�H�t�X�p���ഫ����(II)���p���ഫ���Ƶ{��(III)���ĤG�ӵ{���A�N�p�ߤT���@����{������Ƭ����ơC�`�N: ��ƮɡA�Х���Ƹѵ���z�ȡA��ƫ� z�Ȫ��O��(K3)�Φ�C�����O��(K4)�h����O�d�A����A�� Kout 1(��Kout 2)���� x���� (�� y����) ��Ƭ����ơC
��4: ����p�ߤG���@���誺�Ѭ����ƮɡA�Цb���y�Ȯɫ�AC�פ�{���A�A��Kout 3���Ny����Ƭ����ơA��ƫ� y�Ȫ��O��(K3)�Φ�C�����O��(K6)�h����O�d�A����A�� Kout 1���� x���ȶi����ơC
��5: �p�ߤT���@����{���q�����������t�X�p���ഫ���Ƶ{���C
�@