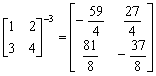二階矩陣的冪(III)

程式由網友roviury提供。

程式更新日期: 2012年1月20日

程式可以計算一個2×2矩陣的冪。 這個程式的速度比第(I)及(II)版快，特別是計算較大數冪時，速度明顯快很多。冪亦可以是正數、負數(包括逆矩陣)及小數。

程式需要在 CMPLX 模式下執行，因此在選擇新程式位置後，按 2 選用CMPLX模式。

程式 (168 bytes)

?→A: ?→B: ?→C: ?→D:

AD - BC→Y: . 5(A+D:

Ans + √( Ans² - Y)cos(π^r(Ans<0→M:

?→X: If Abs(Ans: Then Y÷M²→Y:

A÷M→A: B÷M→B: C÷M→C: D÷M→D:

Abs(M)^(X)∠(Xarg(M→M: IfEnd: X:

If Y≠1: Then Abs( Y => Ans^(X)∠(X arg( Y: (1-Y)^-1( 1-Ans: IfEnd:

MAnsM- →Y: AY + M→A◢ BY→B◢

CY→C◢ DY + M→D

註1: 如想計算逆矩陣，只要輸入負冪數即可。

註2: 如果將紅色的 : 改為◢ 可以顯示出 alpha 及beta 值。

例題1: 計算

按 Prog 1 再按 1 EXE 2 EXE 3 EXE 4 EXE 3 EXE (顯示37)

EXE (顯示54) EXE (顯示81) EXE (顯示118)

所以

例題2: 計算

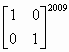
按 Prog 1 再按 1 EXE 0 EXE 0 EXE 1EXE 2009 EXE (顯示1)

EXE (顯示0) EXE (顯示0) EXE (顯示1)

所以

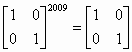
例題3: 計算以下矩陣的逆矩陣:

按 Prog 1 再按 1 EXE 2 EXE 3 EXE 4 EXE - 3 EXE (顯示 - 14.75)

SHIFT d/c (顯示 -59/4) EXE (顯示 6.75) SHIFT d/c (顯示 27/4)

EXE (顯示 10.125) SHIFT d/c (顯示 81/8)

EXE (顯示 -4.625) SHIFT d/c (顯示 -37/8)

註: 若不用顯示假分數，可以省略不按 SHIFT d/c。

所以

返回 CASIO fx-50FH、fx-3650P II、fx-50FH II及fx-50F PLUS 程式集