二階矩陣正整數冪(II)

程式是由網友SuperMANganese提供，程式可以計算一個2×2矩陣的正整數冪。 這個程式的速度比第(I)版快，特別是計算較大正整數冪時，很明顯比第(I)版快很多。

網更新日期: 2011年12月30日

程式需要在 REG Lin 模式下執行，因此在選擇新程式位置後，按 5 1 選用REG Lin模式。

注意: 藍色的英文字為統計模式中的變數(Σx 按 Shift 1 2，Σy 按 Shift 1 → 2，n 按 Shift 1 3)，要特別留意Σx² 是先按出統計變數Σx，然後再按平方鍵 x²，而不是直接按出統計變數Σx²。

程式 (202 bytes)

FreqOn: ?→A: ?→X: ?→Y: ?→D: ?→M:

Y→B: D→C: A÷M , X÷M ; M DT: 1→A:

Rec( 0 ,  0: 1→D: Fix 0: While 1:

If .5n-Rnd(.5n: Then BA+CY→M: ΣxA+ΣyY→A:

M→Y: ΣxX+ΣyD→M: BX+CD→D: M→X:

n≦1 => Break: IfEnd: BΣx+CB→M: Rnd(- .5n:

Ans^-1(Σx² + BΣy - Σx , Ans^-1(ΣxΣy + ΣyC- Σy ; Ans DT:

If B: Then Σx + B^{2 -1}(2MBC - M²→C: Else C²→C: IfEnd:

M→B: WhileEnd: Norm 1: A◢ X◢ Y◢ D

註1: 冪數越大時，計算時間會較長。

註2: 程式限制為冪數小2²⁶，若果希望同時計算逆矩陣(負整數冪數)，可在程式尾加入程式碼 ◢ 1┘(AD - XY→B:

DB◢ -XB◢ -YB◢ AB，程式長度則變為 230 bytes。

註3: 程式原理 --- 此程式使用對冪數m分解為由2的冪數組成，

即m=a₀ 2⁰+ a₁ 2¹ + a₂ 2² + ...+ a_k 2^k ，其中a₀ , a₁ , ... , a_k = 0 或 1 及 a^k ≦m。

例如: 100=2² + 2⁵ +2⁶ ， 而矩陣P的正整數冪 P^m = (P^( a₀ 2⁰ ))(P^( a₁ 2¹ ))(P^( a₂ 2² ))...(P^( a_k 2^k ))
例如: P¹⁰⁰ =(P⁴)(P³² )(P⁶⁴) ， 此程式利用此方法計算P^m， 對任何正整數ｍ，此程式進行矩陣乘法運算的次數≦ 1+2(lnx)/(ln2)， 對一些較大的正整數m會運算會明顯比第(I)版快。
　

例題1: 計算

按 Prog 1 再按 1 EXE 2 EXE 3 EXE 4 EXE 3 EXE (顯示37)

EXE (顯示54) EXE (顯示81) EXE (顯示118)

所以

例題2: 計算

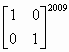
按 Prog 1 再按 1 EXE 0 EXE 0 EXE 1EXE 2009 EXE (顯示1)

EXE (顯示0) EXE (顯示0) EXE (顯示1)

所以

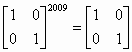
註4: 計算例題2，本程式計算時間大約為17秒，若果改用第(I)版(舊版本)，計算時間則大約為810秒。

返回 CASIO fx-50FH、fx-3650P II、fx-50FH II及fx-50F PLUS 程式集